MCMC estimation in MLwiN
Markov Chain Monte Carlo (MCMC) methods allow Bayesian models to be fitted, where prior distributions for the model parameters are specified. By default MLwiN sets diffuse priors which can be used to approximate maximum likelihood estimation.
Two procedures are used by MLwiN. Gibbs sampling is used with Normal responses and the Metropolis-Hastings algorithm with Normal or binary/proportion responses - these are the only ones available in release 1.0.
Estimation is controlled using options that appear on the toolbar when MCMC is selected or the estimation control button is pressed. The following items can be controlled.
Burn in
This is the number of initial iterations which will not be used to describe the final parameter distributions; that is they are discarded to allow Markov chain to converge to the posterior distribution.
Monitoring
After the burn in period, the monitoring period is the number of iterations, after which distributional summaries are to be produced.
Refresh
This specifies how frequently the parameter estimates are refreshed on the screen during iterations.
Thinning
This is the frequency with which successive parameter values in the Markov chain are stored.
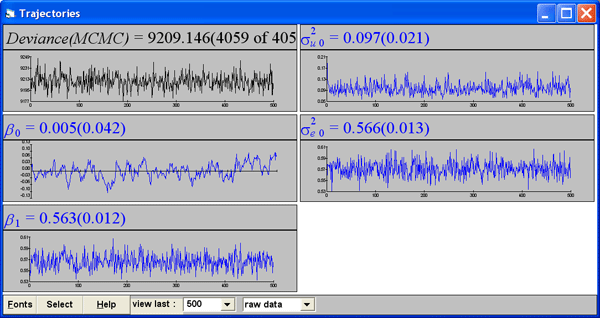
For Metropolis-Hastings there are some additional parameters to be set. While iterations are taking place you can view their progress in a trajectories window such as the following for a random coefficient Normal model:
Monitoring MCMC estimation
MCMC methods allow Bayesian models to be fitted with prior parameter distributions. By default MLwiN sets diffuse priors. Both Gibbs sampling and Metropolis Hastings sampling can be used.
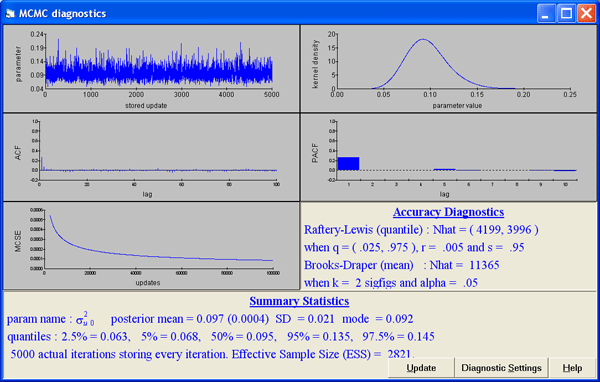
We can obtain summary measures and diagnostics by clicking on any of these graphs - and obtain a window such as the following which shows a kernel density plot, autocorrelation functions and estimates of required chain length etc. for the level 1 variance parameter: If an informative prior had been specified the distribution would be superimposed on the posterior kernel density.