Centre for Multilevel Modelling

menu

Random slope models

A transcript of random slope models presentation, by Rebecca Pillinger

Allowing for different slopes between groups

We have seen how random intercept models allow us to include explanatory variables and we saw that, just like with the variance components model, in the random intercept model, each group has a line, and we saw that the group lines all have the same slope as the overall regression line.  And remember that was true for the variance components model as well, because in that case all the lines were flat, they just had slope 0.  So, for the random intercept model, in every group, the effect of the explanatory variable on the response is the same and that's actually one of the assumptions of the random intercept model. 

But is it always valid?

Random intercept model fitted to example data

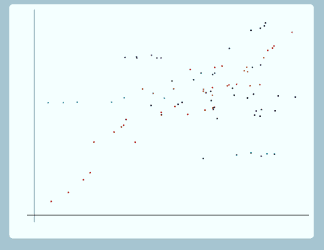
Scatterplot of some data points in various colours

Well here is a possible situation we could have, we've got some data points here, and we can imagine that these are exam results for pupils within schools, so along the x axis, we have previous exam score, and along the y axis we have exam score at age 16 and we want to fit a random intercept model to this data.

Overall average line and group lines from random intercept model superimposed over scatterplot

So here's our random intercept model and we fit it to our data and in order to better be able to examine how well that model fits the data, we're just going to highlight four of the groups and look at those.  So if we look at the red group, here, you can see that for this group, the points are following a line with a steeper slope than the group line that we've drawn in, and again for the dark blue group, the points seem to be following a line with a steeper slope than the group line that we've drawn in.  On the other hand for the light blue group, the points seem to be following a line with a shallower slope than the group line that we've drawn in.  And for the green group as well, the points seem to be following a line with a shallower slope than the group line that we've drawn in.

The assumption of equal slopes

So for this data, for some groups, the explanatory variable has a large effect on the response and for others it has a small effect.  So clearly the random intercepts model, with its parallel group lines, is not doing a very good job of fitting the data. 

So that's all very well in theory, but you might wonder, does this actually happen in practice?  Well, in fact, in exactly the example we've been considering, pupils within schools with response being exam score, and explanatory variable being previous exam score, some investigators have found that their data behaves like this. So that for some schools pretest has a large effect on the response and for others the effect is smaller.  But on the other hand, other investigators with exactly the same situation, pupils within schools; response: exam score; explanatory variable: previous exam score, have found that for their data, the random intercepts model is a perfectly good fit: it doesn't appear that the relation between the explanatory variable and the response is different for different schools.  And also it's important to bear in mind that for some datasets, there's only enough power to fit a random intercepts model in any case.  So what this tells us is that sometimes the random intercept model does fit well to the data and we don't want to look any further, that's perfectly adequate, but in other cases the random intercept model doesn't fit well and we need something else.

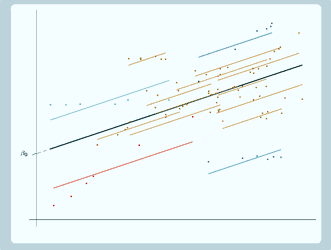
So for the data we've just been looking at, what we really want is a model that looks like this. 

‌

So this is a random slopes model and we can colour in the other groups as well.  You can see that this is actually fitting the data better than the random intercept model did because you can see for example for the red group, the group line now does seem to have the same slope as the line that the points are following, and for the light blue group as well, the group line seems to have the same slope as the line that the points are following, and the same for all the other groups.  And we can extend those group lines as well, the model doesn't specify how long those lines are, they extend infinitely, but, as you can see, drawing it like that does look a bit complicated and confusing, it's kind of hard to see what's going on there. So we mostly will not extend the lines when we draw it on future slides.

The random slopes model

So what's the difference between a random intercept model and a random slope model? 

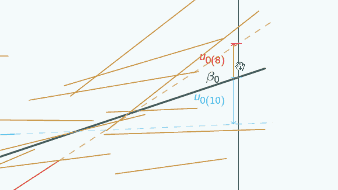
Well, unlike a random intercept model, a random slope model allows each group line to have a different slope and that means that the random slope model allows the explanatory variable to have a different effect for each group.  It allows the relationship between the explanatory variable and the response to be different for each group.  So how do we actually achieve that in terms of the model equation? Well what we do, is to add a random term to the coefficient of x1 so that it can be different for each group.  So for the random intercept model we have β0, we have β1x1, we have u0 and we have e0.  For the random slope model we have added in this u1x1, This u1 is different for every group, so that means that this coefficient is different for every group.  So that means that the relationship between x1 and y is different for every group. Usually, though, we actually rearrange this equation, so we multiply out this bracket, and β1x1comes into the fixed part of the model and u1x1 comes into the random part of the model.  Now note that we've actually only introduced one extra thing in this model, compared to the random intercept model, we've only introduced this u1, but we've actually got two extra parameters to estimate, we've got σu01 and we've got σ2u1, and that's something we're going to come back to shortly. 

So, what do our u1 and our u0 look like in our random slopes model?

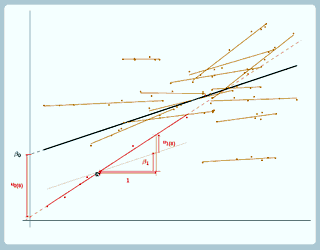
Overall average line and group lines with different slopes superimposed over scatterplot, one group is highlighted in red and where the parameters, beta_0, beta_1, u_0 and u_1 impact the line is shown.

Well, our u0 looks just the same as for the random intercept model, it's still the difference between the intercept for the overall line and the intercept for the group line, so just this difference here. u1 is the difference between the slope for the overall line and the slope for the group line.  So, to be able to be able to better see what u1 is we've actually drawn faintly here a line parallel to the overall line.  It's not really part of the model, this, we've just drawn it on so it's easier to see what u1 is. So for this line with the same slope as the overall line: well, the slope is β1  as it's the same as the slope for the overall line, and u1 is the difference between the slope for the overall line and the slope for the group line.  So the slope for the group line is this, so u1 is the difference between the slope for the group line and the slope for the overall line.  If we look at the light blue group now, again u0 is the difference between the intercept for the overall line and the intercept for the group line, this difference here, and now for this group, the group line has a shallower slope than the overall line

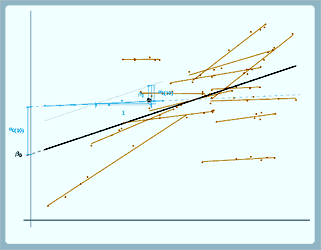
Overall average line and group lines with different slopes superimposed over scatterplot, one group is highlighted in blue with a shallow slope and where the parameters, beta_0, beta_1, u_0 and u_1 impact the line is shown.

(again we've drawn a line parallel to the overall line so you can compare easily).  So again for the overall line the slope is β1.  Now because the group line has a shallower slope, we actually have to come back down again to get the slope of the group line, so we've got a negative u1 here.

Interpreting the parameters

So how do we interpret the parameters? 

Well, β0 and σ2e0can be interpreted just the same as for the random intercepts model, so β0 is still the intercept of the overall line, σ2e0 is still the level 1 variance.  β1 now, is the slope of the average line, so it's the average change (that's the average across all groups) in y for a 1 unit change in
x1.  σ2u0, σ2u1

and σu01

are a bit more complicated to interpret.  Basically σ2u1is the variance in slopes between groups; σ2u0 is the variance in intercepts between groups - and that means it's also the level 2 variance when x=0;  σu01 is the covariance between intercepts and slopes.  But we can't interpret them separately, we have to interpret them all together, and we'll explain why that is, after we have a look at what this covariance between intercepts and slopes means.

Covariance between intercepts and slopes

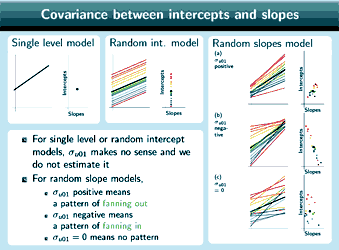
Slide containing 3 graphs that illustrate a single level regression (graph a), a random intercept model (graph b), and random slopes model (graph c)

So here's one example of a random slopes model. So this is not looking at the same data we were looking at before. 

So in this particular case [see graph (a)], the lines are showing a pattern of fanning out, they are more tightly grouped here and more spread out here. So in this particular case, the lines which have the larger intercepts here also have the larger slopes, so the lines with larger u1, larger slopes, have larger u0, larger intercepts.  So if we plot the intercepts against the slopes, you can see this pattern of positive correlation, so σu01 is positive in this case. 

In this situation [see graph (b)], we've got again some different data, the lines are showing a pattern of fanning in, so in this case, the lines with the larger slopes, larger u1, have smaller intercepts, smaller u0, and again if we plot the intercepts against the slopes, now σu01 is negative. 

The third possibility [see graph (c)], again with some different data, is where the lines show no pattern, so in this case, if we look at the lines with larger intercepts, we can't say that they have larger slopes or smaller slopes: there doesn't seem to be a relation between intercepts and slopes, and if we plot the intercepts against the slopes again here, you can see that there doesn't appear to be any pattern.  So in this case
σu01 is 0. 

So you might be wondering, what about the random intercepts model, why didn't we talk about this when we were looking at the random intercepts model? Well, for the random intercepts model [see graph top middle], all of the lines have the same slope, they are parallel, no matter what their intercept, so there's no actual variation in slope (we can see that if we plot again the intercepts against the slopes, there's only one value of the slope) so it doesn't actually make sense to take the covariance between intercepts and slopes in this case, and anyway it's hard to see how we could estimate σu01 because we don't have u1 in this model.  So it doesn't make sense to estimate the covariance between intercepts and slopes and we don't estimate it.

Again for the single level model [see graph top left ], there's only one line for the single level model, we just have the overall regression line and so again, if we plot the intercepts against the slopes, you can see we've only got one point, so again it doesn't make sense to take the covariance between intercepts and slopes, anyway we don't have u0 or u1 for this model so it's hard to see how we could estimate σu01. For the single level model as well, we don't estimate the covariance between intercepts and slopes. 

To sum that up, for single level or random intercept models, the covariance between intercepts and slopes doesn't make any sense and we don't estimate it.  For random slope models, σu01positive means a pattern of fanning out, σu01negative means a pattern of fanning in and σu01=0 means no pattern.  So OK, in this situation, for all of our different datasets, we've had the overall relationship between the explanatory variable and the response being positive, we've had a positive β1.  You can see that if you look at the overall line which is the thicker line in the middle of each of these graphs. 

What about if β1 had been negative? 

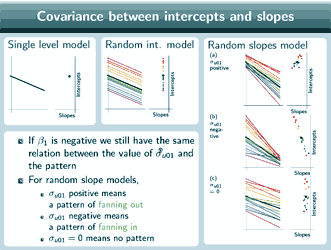
Slide containing 3 graphs that illustrate, this time with a negative slope, a single level regression (graph a), a random intercept model (graph b), and random slopes model (graph c)

Well, here's the situation when  β1 is negative, and actually it turns out that the relationship between this covariance and the pattern is exactly the same, so still for random slope models, σu01positive is a pattern of fanning out, still σu01negative is a pattern of fanning in, and still σu01=0  is no pattern.

The scale of x

OK so we move on now to the question of the scale of x because this actually turns out to be quite relevant in interpreting this covariance.  When we collect or analyse data, we always choose the measurement scale of x.  That involves two choices: so first of all what the units are, so for example are we going to measure height in centimetres or metres? And, in other words, how big is 1?  And the second question is, where the scale is located, so if we want to measure temperature, do we choose to put zero at freezing point or do we choose to put 0 at absolute zero? So in other words, where is 0?

So as an example of that, suppose that we want to measure exam score.  We have several choices.  We could use the raw number of marks, so in that case, for example, full marks might be 60.  We could use percentages so now full marks would be 100.  We could use a scale where 0 is 50% right and 50 is full marks. So that would have the same unit size as for percentages, but we'd be centring around 50%.  We could use a scale where the mean mark is 0 so that's centring around the mean.  We could use a standardised scale, so in that case, still the mean mark is 0, but now the variance is 1.  So, these last three choices in particular, you might be quite familiar with these as things you might want to do when you are analysing data and fitting a regression model.  So it's important to remember that these are not just choices that are made when the data is collected, these are also choices that we make when we actually analyse the data.

So what difference does it make to the parameters what scale we choose for x? 

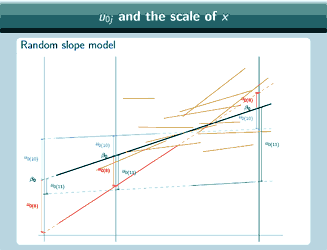
Parameters and the scale of x

Well, for the slope parameters, β1, well β1 will depend on the units that we choose for x1, so it will depend on whether we measure height in centimetres or metres, and that idea is probably already familiar from simple regression: we know that if we measure height in metres, we're going to get a different estimate for β1 than if we measure height in centimetres, and we're used to remembering that when we interpret our estimate for β1. But β1 won't depend on where we place x=0 and the same is also true in fact of u1, that also depends on the units, but not on where x=0 is.

So what about the intercepts?  Well, β0, the intercept of the overall line, will depend on where we place x=0, but it won't depend on the units that we use for x, and again that's probably quite familiar from regression: we're used to the idea that if you centre the explanatory variable before putting it into the regression model, you're going to get a different estimate for the intercept than if you put in the variable without centring.  So the intercept will depend on whether we measure temperature in Celsius or Kelvin for example, but it won't depend on whether we measure height in centimetres or metres. 

u0 doesn't depend on the units that we use for x, but does it depend on where we place 0?  Well actually it depends on which model we fit. 

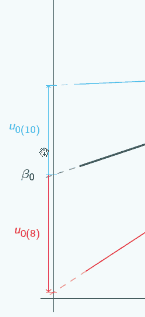
So here's a random slope model

A random slope model

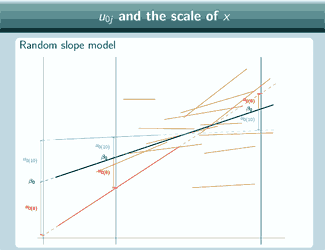
Slide showing a graph of a random slopes model with 3 different x axes illustrated and 2 groups focussed upon (red and blue)

It's actually the same one that we looked at at the beginning, and in this graph we've chosen three different places to put x=0 and we've marked them with vertical lines, and for each place that we could put x=0, we've put on u0, so if we put x=0 here

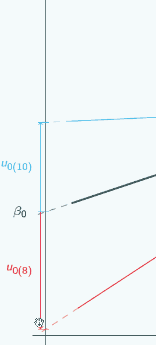Enlargement of random slopes model graph around left most x axes to illustrate 2 u_0is then for the red group, u0 is quite large and negative, for the blue group it's still quite large and positive. 

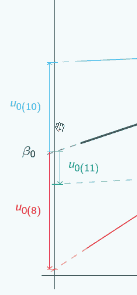
If we put x=0 here,

Enlargement of random slopes model graph around second of the x axes to illustrate 2 u_0is

then for both groups, u0 has got smaller but the signs have stayed the same. 

If we put x=0 here

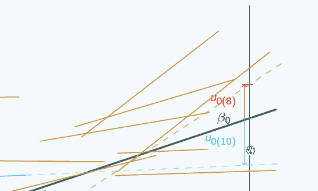Enlargement of random slopes model graph around right most x axes to illustrate 2 u_0is and how they changes sign. you can see now the signs have actually swapped. Here u0 is positive for the red group,

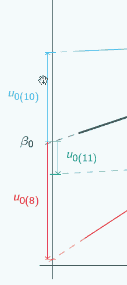
but here 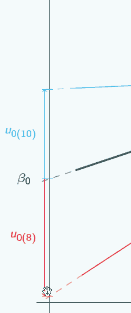Enlargement of random slopes model graph around left most x axes where red group u_0 is negative and here 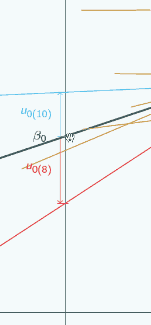Enlargement of random slopes model graph around middle x axes where red group u_0 is negative it was negative,

and here

Enlargement of random slopes model graph around right most x axes where blue group u_0 is negativeu0 is negative for the blue group,

but here

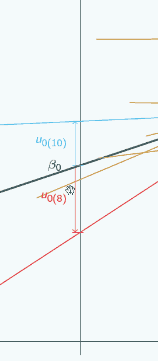Enlargement of random slopes model graph around left most x axes where blue group u_0 is positive and here Enlargement of random slopes model graph around middle x axes where blue group u_0 is positive it was positive,

so clearly it is going to make quite a difference to our estimate of u0 where we decide to put x=0.

If we put on the green group now

Slide showing a graph of a random slopes model with 3 different x axes illustrated and 3 groups focussed upon (red, blue and green)

we can see that actually the relationship between u0 and where we put
x=0 is even more complicated than just looking at the red and the blue group might suggest. Because for the red and the blue group, here

Enlargement of random slopes model graph around left most x axes where red and blue group u_0s and large in magnitude u0 is quite large,

it gets smaller if we put x=0 here 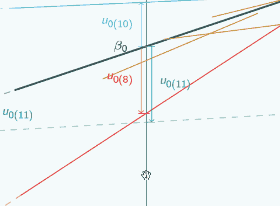Enlargement of random slopes model graph around middle x axes where red and blue group u_0s and smaller in magnitude

and then if we put
x=0 here 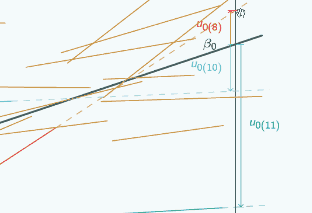Enlargement of random slopes model graph around right most x axes where red and blue group u_0s switch signs the sign changes, but actually the green group doesn't follow that same pattern. 

For the green group, if we put x=0 here

Enlargement of random slopes model graph around left most x axes where green group u_0 is small in magnitude u0 is quite small,

if we put x=0 here 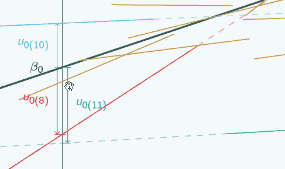Enlargement of random slopes model graph around middle x axes where green group u_0 is large in magnitude u0 is bigger,

and if we put x=0 here

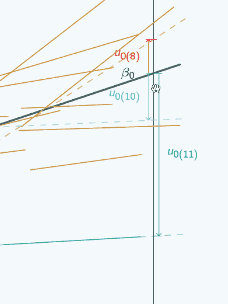Enlargement of random slopes model graph around right most axes where green group u_0 is larger still in magnitude u0 is bigger still and it hasn't changed sign. 

So this shows that the relationship between u0 and where we put x=0 is actually quite complicated and it's not necessarily going to be simple to correct for where we put x=0 and get some kind of overall estimate for u0 that somehow doesn't depend on where we put x=0, we really are, when we interpret our estimates of u0, going to have to take into account where we've put x=0 and interpret the estimates in light of that.

OK, so what about for the random intercept model now?

Random intercept model

Well, for the random intercept model, actually it doesn't make a difference where we put x=0 as to what estimate we'll get for u0, so again you can see that we've done the same thing here, for the red group now you can see that no matter where we put x=0, u0 is exactly the same, and for the blue group, u0 is exactly the same no matter where we put x=0.  For the green group, as well, u0 is exactly the same no matter where we put x=0.  And actually this is something that, although we didn't actually directly mention it, when we were talking about random intercept models, we kind of implicitly assumed it because when we were interpreting our estimate of u0  and our estimate in particular of σ2u0 we didn't consider where we put x=0, that didn't come into our interpretation at all, and that was OK because, as we can see, actually it doesn't make a difference.

Random intercept model - example

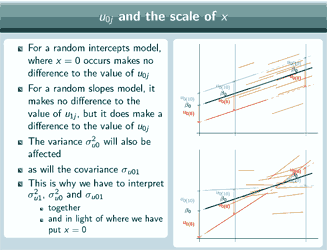
Slide showing graph of a random intercept model with overall regression line and several parallel group lines.

So for the random intercepts [model] where x=0 is makes no difference to the value of u0 but for a random slopes model it makes no difference to the value of u1 but it does make a difference to the value of u0.  And that means that the variance, σ2u0 will also be affected as will the covariance, σu01 and that's why we have to interpret σ2u1, σ2u0 and
σu01 together and in light of where we have put x=0. 

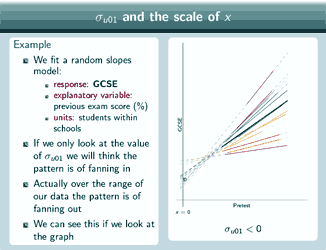
Slide with text repeated below and recap of graphs of the random intercept and random slopes models.

So as an example of that, imagine that we fit a random slopes model and again we're fitting it to pupils within schools and our response is GCSE, our explanatory variable is previous exam score, measured in % so x=0 means nothing right, and yes, our units are students within schools. And so imagine that our data is as we can see at the right here.  So if we only look at the value of σu01, well σu01is negative, the lines with the larger intercepts have the shallower slopes, lines with smaller intercepts have larger slopes, so we'll think that the pattern is of fanning in.  Actually over the range of our data, that's where the lines are thick and not dotted, that's where we actually have points in our dataset, the pattern is actually of fanning out. So this negative value for σu01 has given us totally the wrong idea about the shape of our data.  We can see that by looking at the graph.  And that's because actually over here, there is a pattern of fanning in, this negative covariance is correct for this range of values, which are not the range we actually have in our dataset.  If we put x=0 here, we'd get an estimate of σu01 that was 0 and if we put x=0 here, we'd get an estimate of σu01 that was greater than 0 so that would actually correspond to the pattern of fanning out that we see in our data.  So, when we actually get our estimates for the model, as well as looking at the value of σu01, and seeing whether it's positive or negative or close to 0, it's important to also plot our estimated group lines for our data so that we can actually see what the pattern is for the range of our data and that's something that we're going to come back to later in the section on prediction.

So what research questions can we answer using a random slope model? 

Examples of research questions

Well, here are some examples.  So in this study [Clark et al, 1999] they looked at the research question: Is there a large amount of variability between subjects in the rate of change in Mini Mental State Exam (MMSE) score? So they had subject at level 2 and occasion at level 1, their random slope was on year and their answer was yes.  Mini Mental State Exam is actually used to assess patients who have been diagnosed with Alzheimer's disease and the authors were actually interested in this question because they wondered whether it's a good measure, and they actually decided that it wasn't, largely because of this large amount of variability in slope between subjects.  Also, it's interesting to note that there was a correlation between its slopes and intercepts of 0.33 for their data so that means that subjects with higher intercepts had less decline in MMSE score. 

This study [Tymms et al, 1997 ] looked at whether the effect of attainment at the start of school on attainment after the first year of school varies across schools.  They were looking at children who were just starting school for the very first time.  So they had school at level 2 and pupil at level 1 and their random slope was on pretest and their answer was yes, the effect does vary across schools.  They did comment, though, that the variability in slopes that they found could be due to ceiling effects of their post test: in some schools the pupils scored so well to begin with, before entering the school, that there wasn't really anywhere for them to go on the assessment at the end of school.

In this example [Polsky and Easterling, 2001] they looked at the question of whether districts vary in their sensitivity of land value to climate, so they were looking at districts in the US Great Plains area and their climate measure was mean maximum July temperature over 30 years and they were looking at land value but what they were actually interested in was land use - land value was a proxy for land use because different crops have different prices so that kind of measures land use.  So, they had districts at level 2 and county at level 1 and their random slope was on this measure of mean maximum July temperature and their answer was: Yes, the districts do vary in the sensitivity of land value to climate.  And they actually went on to fit a model which showed that counties in districts which had more variability in temperature from year to year (they had a measure of this) actually benefit more from high July temperatures.  But that's a more complicated model than we are going to look at in this particular set of presentations.

This example [Jex and Bliese, 1999] looked at whether there is variability across army companies in the relationship between hours worked and psychological strain.  So they had company at level 2 and soldier at level 1 and the random slope was on hours worked and their answer was: Yes, there is variability across companies. And they also went on to fit a more complicated model to try to explain this.  They wondered whether the variability could be explained by differing beliefs in the efficacy of the company across companies - so - how effective that company would be at solving the tasks presented to it. But they actually concluded that that didn't explain the variability.

And here are the details of those studies:

Calculating the total variance

Slide with text that explains the formulae for the variance functions at level 1 and level 2 and hence for the VPC for a random slopes model.

In the presentation, 'Fitting and interpreting a random slope model', we mentioned that we can't interpret the level 2 random parameter estimates separately, we have to interpret them together - so that's the variance of the slopes, the variance of the intercepts, and the covariance between the intercepts and slopes - those three parameters have to be interpreted together. And we're going to see how to do that now because the way to interpret them together is to calculate the level 2 variance. 

So, if we look at the level 1 variance first of all, that's quite simple.  We only have one random term at level 1, we just have e0.  So the level 1 variance is just σ2e0. 

For the level 2 variance we've got two random terms at level 2.  We've got u0 and we've got u1x1.  So the level 2 variance is going to be the variance of ( u0 + u1 x1) so that actually works out as the variance of u0 plus 2 times the covariance between u0 and u1 x1, plus the variance of u1x1. And that's σ2u0 because we defined the variance of u0 to be σ2u0; plus 2 times σu01, because we defined the covariance between u0 and u1 to be σu01, times x1; plus σ2u1 because that's the variance of u1 (we defined it to be that) times x12.  And notice that the level 2 variance is now a quadratic function of x1.  So for the random intercept model, the level 2 variance was just σ2u0, so that was just constant, no matter what value of x1 we had. But for the random slopes model, the level 2 variance actually depends on the value of x1, it is actually a quadratic function of x1. 

So the variance partitioning coefficient is also going to depend on x1 now, so the variance partitioning coefficient is still the level 2 variance divided by the total residual variance and so here's the level 2 variance on top  here just as we calculated it here and on the bottom we've got the level 2 variance again plus the level 1 variance.  And we could actually plot the level 2 variance against x  to examine how it changes with different values of x. We also could plot the variance partitioning coefficient against x  to examine how that changes, but we're going to get pretty similar information from either of those plots so it's probably only worth doing one of them.

Hypothesis testing for the random slopes model

Well, it's actually pretty much the same as for the random intercepts model.  So for the fixed part, our estimate of βk is significant at the 5% level if the modulus of βk divided by its standard error is >1.96, so that's also just the same as the single level regression model.  For the random part, again we need to use the likelihood ratio test, so this time we're comparing the model with u1x1 to the model without u1x1.  So we're basically just comparing the random slope model, that's the model with u1x1, with the random intercept model, that's the model without u1x1. So those two models are exactly the same in terms of explanatory variables, the only difference is that the random slopes model has this u1x1in it.  So again the test statistic is 2 times the log likelihood of the first model minus the log likelihood of the second model and this time we have 2 degrees of freedom because we've got 2 extra parameters in the first model compared to the second model: we've got σ2u1 this time and σu01.  So we compare the test statistic against the chi2(2) distribution with 2 degrees of freedom, and again we can divide the p-value by 2 if we want.  So the null hypothesis is that σ2u1 and σu01 are both 0 and if that's the case than a random intercept model would be more appropriate than a random slope model.

Let's now return to the technicalities of the model and have a look at what assumptions we are making when we fit the random slope model. 

Slide showing in equation form the assumptions of the random part for a random slopes model that are repeated in text below.

Well, we have all the same assumptions that we had for the random intercept model, and in addition, we assume that the slope residuals for two different groups are uncorrelated; we assume that the covariance between the intercept and the slope residual for the same group is σu01 and that the intercept and slope residuals for different groups are uncorrelated, and we assume that the slope residual is uncorrelated with the level 1 residual and that the slope residual is uncorrelated with the covariates.

The correlation matrix

If we want to look at the correlation matrix now

Well, we'll be looking at the correlation again between the value of the response minus the fixed part prediction for each pair of individuals in our dataset, and for the random slope model, the response minus the fixed part prediction comes to this, just the random part of the model. So, what is actually the covariance between this for each pair of individuals in our group?  Well, when we're looking at the same individuals, so the diagonal elements of our covariance matrix, the covariance between these terms is actually just the total variance, here's the level 2 variance plus the level 1 variance, and for two elements from different groups, this covariance is just 0.  But if we want to look at the covariance for two different individuals from the same group, so the intraclass correlation, that's actually a bit more complicated. 

For a random intercept model, the intraclass correlation was identical to the variance partitioning coefficient, and it was quite simple to calculate.  For a random slopes model, the intraclass correlation is not equal to the variance partitioning coefficient because the intraclass correlation will depend on the value of x1 for each of the two elements in question.  The variance partitioning coefficient just depended on one value of x1 but if two different people each have a different value of x1, both those values are going to go into the formula for the intraclass correlation.  The exact expression for the intraclass correlation is quite complicated; we're not going to give it here because the important thing is simply to note that the intraclass correlation will depend on the two values of x1 as well as σ2u1, σ2u0 and σu01.

So let's now look at predictions for the random slope model

Predictions for the random slope model

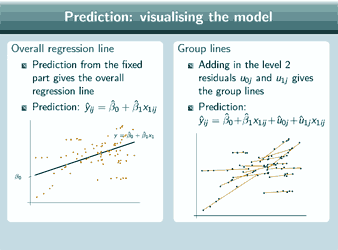
Slide talking about how to visualise predictions that contains one plot of the overall regression line and another plot showing the individual group lines.

And remember that in the presentation about fitting and interpreting a random slope model, when we were talking about interpreting the covariance between intercepts and slopes, we mentioned that it's very important, as well as just looking at the estimate, to plot the predicted group lines in order to interpret that estimate properly and so now we're actually going to show how to do that. So the fixed part prediction will give the overall regression line, so the prediction is Beta hat 0 + beta hat 1 x 1 i j and here's the line that we get. 

For the group lines, we have to add in the level 2 residuals to our fixed part prediction and that will give us the group lines, so now our prediction is Beta hat 0 + beta hat 1 x 1 ij + u hat 0 j + u hat 1 j x 1 ij and here are the group lines that we get.  And we can add on the data points to both of those predictions to see how well those lines are fitting our dataset. And we can obviously combine both those predictions on the same graph, if we want, to get an overall picture of our model, and if we do that, this is what we get and we can add on the data points again. 

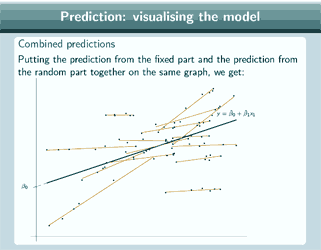
Slide containing a graph that shows both the overall regression line and individual group lines.
So there's a picture of our random slope model, and now we can check whether our data shows a pattern of fanning out or fanning in, or, as in this particular example, no pattern.

Random slope models and random intercepts

[We'll] talk now about random slope models and random intercepts because there's a few points here that can be confusing.  So first of all, a matter of terminology.  So this random slope model here, that we've been looking at in these presentations, does have a random intercept as well as the random slope, so that means that technically it is also a random intercept model, it's not wrong to call this a random intercept model.  But, in practice, usually when we use the term, 'random intercept model', we mean a model which only has a random intercept and not a random slope as well. 

Do we always have to add a random intercept to a random slope model?  Well, so far we've always shown a  random intercept in our random slope model and if we left the random intercept out, that would mean that all of the group lines crossed at
x=0, and if we actually have a good reason to believe that the group lines should cross at
x=0, then we can fit a model without random intercepts.  But usually we don't have a good reason to believe that so usually we do put the random intercept in. 

Multiple explanatory variables

So what if we want to put multiple explanatory variables in our model? 

Slide that shows equations for a random slope model with firstly one predictor variable and then many predictor variables

So far, we've only looked at a model with one explanatory variable,  but if we want to have more than one explanatory variable, then what does that mean for our random slope?  Well, we can actually put a random slope on just one of our explanatory variables or we can put a random slope on several of them as in this example.  Or we can even put random slopes on all of our explanatory variables. But, depending on the number of level 2 units in our dataset, in practice we may not have enough power to put a random slope on more than one explanatory variable.  So, in theory, we can put random slopes on as many or as few of our explanatory variables as we want but in practice there may be some restrictions to how many random slopes we can fit. 

We can put random slopes on interaction terms, we can put them on categorical variables as well, we just add the slope to the dummy variable in that case.

Feedback

Edit this page