Lessons
Over the last five years LISFLOOD-FP has been used in a range of fluvial and coastal flooding studies and the following summarises what we have learned about flood inundation in general and this class of model in particular. Lessons have been learned in four main areas:
- Calibration, validation and benchmarking studies
- Scaling behaviour
- Uncertainty analysis
- Adaptive time stepping
Calibration, validation and benchmarking studies
LISFLOOD-FP has so far been validated for five river reaches: the Meuse in the Netherlands (Bates and De Roo, 2000), the Thames in the UK (Horritt and Bates, 2001a; Aronica et al., 2002), two sections of the the Severn in the UK (Horritt and Bates, 2001b; Horritt and Bates, 2002) and the Imera basin in Sicily (Aronica et al., 2002). In each case the modelled inundation extent has been compared to a flood extent maps derived from either air photography, satellite Synthetic Aperture Radar images or ground survey. The data sets represent the best inundation extent information currently available. The flow routing performance of the model has also been analysed in the case of the Meuse and the Severn. In addition, for the many of these studies the model as benchmarked against other standard hydraulic codes as detailed in Table 1. In each case the ability of the model to predict inundation extent is compared in terms of the measure:
![]()
Where Aobs and Amod represent the sets of pixels observed to be inundated and predicted as inundated respectively.
| Reach name (and length) | Validation data | Maximum LISFLOOD-FP performance (F) | Number of calibration runs | Benchmarked against … |
|---|---|---|---|---|
| Meuse (35 km) | Air photo inundation extent, SAR inundation image, point hydrometry | 82% | 1 | TELEMAC-2D, planar lid approximation to free surface |
| Thames (3 km) | Air photo inundation extent, SAR inundation image | 84% | 25 | TELEMAC-2D, planar lid approximation to free surface |
| Upper Severn (60 km) | SAR inundation images for two events, point hydrometry | 73% | 500 | TELEMAC-2D, HEC-RAS, planar lid approximation to free surface |
| Imera (15 km) | Ground surveyed flood extent | 85% | 500 | - |
| Lower Severn (15 km) | 4 Airborne SAR scenes througha single event | 89-72% | 35 | - |
Table 1 : Summary of LISFLOOD-FP calibration, validation and benchmarking studies for fluvial application.
The model has also been compared to observed extent data for three coastal flooding applications (see Bates et al., in press). Although the data quality is not as good for these tests similar conclusions have been drawn. Results of these studies are outlined in Table 2.
| Area | Type of flooding | Domain size | Grid resolution | Number of cells | Event | Model accuracy (F) | Computational time (on a 2.5 GHz pc) |
|---|---|---|---|---|---|---|---|
|
Towyn, North Wales, UK |
Defence overtopping |
12.5 x 9 km |
50m |
~45k |
1990 |
0.78 |
~60 minutes |
|
Fleetwood, UK |
Defence overtopping |
2.3 x 6.3 km |
10m |
~145k |
1977 |
0.54 |
~5 minutes |
|
North Norfolk, UK |
Defence breach |
40.25 x 42 km |
250m |
~27k |
1938 |
0.91 for the 1938 event. |
~5 minutes |
Table 2: Summary of LISFLOOD-FP calibration and validation studies for coastal application.
From these studies the following general conclusions can be drawn about the fixed time step version of the LISFLOOD-FP model:
- Similar to other storage cell models (e.g. Romanowicz et al., 1996) LISFLOOD-FP is more sensitive to channel than floodplain friction.
- Because the friction coefficients cannot be determined a priori, calibration is a necessity.
- When calibrated against inundation extent data LISFLOOD-FP simulates inundation resulting from an independent event as well as other standard hydraulic models.
- Performance at predicting inundation extent is close to being within the error of the observed satellite or air photo data which we assume to be only capable of classifying correctly 90 % of the true flooded area (see Horritt et al., 2001).
- For the fixed time step model the calibration needs to be optimised depending on whether one wishes to predict inundation extent or flood wave travel time (Horritt and Bates, 2001b).
- Minimal improvement in model performance is obtained by using more complex diffusive wave approximations for the 1D channel and 2D floodplain flow.
In order to test the behaviour of the model with respect to changing grid scale, Horritt and Bates (2001b) conducted a scaling analysis for the River Severn reach discussed above. For the 60 km reach between the gauges at Montford Bridge and Buildwas models were constructed at 10, 25, 50, 100, 250, 500 and 1000m scales. Topography for each was parameterised using a laser altimetry survey made available by the UK Environment Agency. A ~1 in 50 year event which occurred in October 1998 was simulated and calibration studies were undertaken for each model. The results were analysed in terms of model ability to predict inundation extent and flood wave travel time through the reach. This analysis showed:
- Model performance in terms of inundation prediction reached a maximum for the 50 m resolution model. This was virtually identical in the 10 and 25 m models.
- The optimum calibration was stationary with respect to model scale for inundation extent, but non-stationary with respect to scale for wave travel time. This was considered to be due to the changing representation of near channel storage affecting travel time but not extent modelling.
- Model performance in predicting inundation extent was near identical at all grid scales below 250 m if the water levels predicted by the coarse scale model are re-projected back on to the high resolution DEM to reconstruct the detailed shoreline. This implies that only a coarse resolution model is necessary to re-construct water levels in areas of low water surface slope such as floodplains, and that much topographic data need not be included explicitly at the model grid scale.
Given uncertainty over friction values, Aronica et al. (2002) have conducted Monte Carlo analysis of parameter uncertainty for the LISFLOOD-FP code using the Generalised Likelihood Uncertainty Estimation (GLUE) technique of Beven and Binley (1992). Dense sampling of the parameter space for the Thames and Imera models showed that there was no single well defined optimum, and instead a broad region the model’s parameter space provided an acceptable fit to the observed data (see Figure 1). Further, they hypothesised that for different events these regions will be overlapping but not identical. They concluded that:
- Single deterministic predictions therefore represent only one of many ‘behavioural’ model realisations, each of which will give different predictions.
- In reality, the risk of flooding for a particular design event should be conceived as a ‘fuzzy’ map in which there will be significant spatial structure.
Aronica et al. (2002) proposed a method in which the global likelihoods calculated using the F statistics for each model realisation could be mapped back into real space using the measure Piflood:
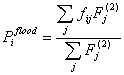
Here we take the flood state as predicted by the model for each pixel for each realisation, and weight it according to the measure of fit F to give a generalised relative risk measure for each pixel (see Figure 2), fij takes a value of 1 for a flooded pixel and is zero otherwise and Fj is the global performance measure for simulation j. Piflood will assume a value of 1 for pixels that are predicted as flooded in all simulations and 0 for pixels always predicted as dry.

Figure 1: Plot of the F performance measure over the parameter space for the River Thames model.
Figure 2: Probability map of predicted inundation, Piflood, for the December 1992 event for River Thames. The observed shoreline derived from interpretation of satellite Synthetic Aperture Radar data is shown as a red line.
Comparison of the fixed and adaptive time step versions of the model against analytical solutions and for real test cases have shown that this version of the model is capable of solving a number of the problems with LISFLOOD-FP identified above (see Hunter et al., in press A and B; Hunter et al., in review). This studies have concluded that:
- Unlike the fixed time step model, the adaptive version showed sensitivity to variations in floodplain friction that appear both intuitively realistic and in line with the sensitivity behaviour of full 2D solutions of the shallow water equations applied to this test site (Horritt and Bates, 2002).
- Whilst parameter sets can be identified for both fixed and adaptive time step models that simultaneously provide acceptable simulations of flood wave travel time and inundation extent, these occur over a broader region of the parameter space for the adaptive time step model.
- Gradients of performance measures over the parameter space are steeper for the fixed time step model than for the adaptive scheme, indicating that the latter code may be easier to calibrate.
- Use of only either inundation extent or travel time data to calibrate the adaptive model results in a rather broad region of the parameter space being identified as capable of providing acceptable simulations. Moreover, use of only inundation extent data in conjunction with a calibration process that seeks to maximise a global measure of fit between observed and predicted inundation resulted in parameter sets being identified as acceptable where the floodplain friction was significantly smaller than channel friction due to trade-offs between the two parameters. This is counter-intuitive as in reality, for most floodplain rivers one would expect this situation to be reversed. Use of both validation data sets was shown to eliminate this problem and also reduce the range of acceptable parameters, and hence the predictive uncertainty.
