A commentary on the secondary school value added performance tables for 2002
released January 2003, updated December 2003
Progress?
Since the routine publication of school league tables started in the early 1990s a principal objection to them has been that they are unfair in that they fail to take account of differential school intakes. Thus, to compare GCSE results of Grammar with Comprehensive schools makes little sense because of the selective nature of the former.
Since 1995 it has been Government’s stated policy to move towards a system of ‘value added’ school comparisons which attempt to deal with this by making suitable statistical adjustments for intake differences. This year sees the first major attempt to implement this for secondary schools and we can therefore begin to evaluate the policy.
Two sets of value added comparisons have been produced; for KS2 – KS3 test scores and KS3 test scores -KS4 GCSE. In future years it is planned to provide KS2-KS4 tables. Thus, only a partial picture can be obtained at present and this needs to be borne in mind when making any interpretations. The results have been produced for individual schools, LEAs and by school type [Comprehensive, Grammar, secondary modern, specialist schools etc. and (undifferentiated) independent schools], although the representativeness of the last category is problematic.
There are 3 key issues which this publication raises. The first arises from the fact that the DfES continues to publish the unadjusted league tables and there is no real attempt to reconcile any differences or similarities. Indeed, there appears to be a strong association between scoring highly on both the unadjusted and the adjusted tables – and I will return to that problem below. Many people will justly find it confusing when confronted with apparently different conclusions. Indeed, given the implicit admission by government that the unadjusted league tables are flawed, one may well ask why they go on publishing them. Thus the schools minister, David Miliband “congratulated those schools that have shown greatest improvement in pupil attainment between 11 and 14 years of age and 14 to GCSE”. One might well ask why his government continues to provide misleading (unadjusted) comparisons for the same schools. Not much progress there, one might conclude.
The second issue is the continuing publication of so called ‘improvement’ measures that compare schools on the basis of changes in scores from year to year. Like the single-year league tables these are unadjusted for intake and therefore suffer from exactly the same drawbacks as the former. Yet ministerial statements do not recognise this.
The third issue concerns the quality of the value added tables and this is what I will now look at in detail.
Value added calculations
There is now a great deal of research experience in the calculation and interpretation of value added data (see value added school performance commentary ) and the most important considerations are as follows. First of all, it is important to ensure that the adjustment for intake scores is adequate; there is evidence that for secondary schools it is important to go back to adjust for performance in junior schools. Secondly, it is very important to provide ‘uncertainty intervals’ for any results that reflect the relatively small numbers of students involved in any one school – this is also a key issue in the ‘raw’ league tables. Thirdly, mobility of students between schools (instability) can seriously affect both value added and raw league table scores. Students who are mobile tend to have different rates of progress and some schools have more mobile students than others. Finally, there is now extensive evidence that schools differ along a number of value added dimensions, most importantly according to the particular intake scores of the students.
The DfES statisticians do point out in a technical note the problem of uncertainty intervals and mention the stability problem. Both of these, however, are in the ‘small print’ and have largely been lost in media coverage. Most importantly, they have been ignored by ministers who have ignored their responsibility to warn users of the limitations of what is published. Of course, if ministers were to stress these limitations of value added tables they would implicitly also be doing so for the raw league tables to which they attach such importance.
One of the results that some find surprising is that there is an apparently strong relationship between raw scores and value added ones with selective (Grammar) schools tending to have the highest value added scores. However, the method of computing the value added scores seems likely to have generated this result. Essentially, the DfES assumption is that each school has just a single value added score that applies whatever the initial intake score happens to be. With this assumption it can be shown that you will in fact obtain the relationship seen. However, research has shown that this assumption of a single value added score is untenable, and the observed relationship in fact may just be a case of having improperly specified the statistical analysis. We should therefore be rather cautious about reading very much into the present results.
The next section summarises the technical issue.
Correlating value added and raw scores
To illustrate the point suppose we have a simple, centered, 2-level value added model
![]() (1)
(1)
with the usual notational conventions and where the random school effects are independent of the intake scores and we have the same number of students, n, in each school. The covariance between the school means and the school effects is given by and the corresponding correlation is given by
 (2)
(2)
Clearly, this correlation is always positive (unless the school level variance is zero and there are no school effects) and decreases as the variance between the average school intake scores increases. The DfES calculations are not based on exactly model (1); instead they use an informal nonlinear smoothing technique for the regression relationship, with value added scores obtained by differencing. Nevertheless, a similar result applies.
If the following, more realistic, model is true and is fitted,
 (3)
(3)
then the value added depends on the intake score and we have several possibilities such as, for example, school A having higher value added score than school B for low intake scorers but vice versa for high intake scorers. Such ‘differential’ effects have been shown often to occur in practice.
If (1) is not the correct model, but, say, (3) is true and we fit (1), the covariance and variance terms used in calculating the correlation will be functions of the intake score means, but we will still, in general, obtain a positive correlation.
Thus, assume additionally that the additional (slope) random effect is independent of the intake scores. If we fit a variance components model then model (3) reduces to

where each school’s 'composite' residual, in brackets, is estimated at the intake score mean, and this leads to a correlation between the school means and the composite residuals given by
 (4)
(4)
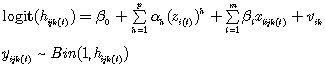
This expression exhibits similar behaviour to (2), decreasing as the variance of the mean intake scores increases and tending towards a constant value

Finally, we note that for model (1) the correlation between the average initial score and the level 2 residual is, by definition, zero. However, for model (3) the correlation between the average initial score and the composite residual is given by

which will always be positive unless the variance between the mean intake scores is zero. Thus, a failure to model the (random coefficient) relationship correctly will tend to lead to spurious conclusions.
Some conclusions
The current system of publishing performance tables is still very flawed. The fact that some advance towards more realistic results seems to be taking place is to be welcomed, but only if policymakers admit the current limitations and are open with the public about what it is and is not possible to infer from the data.
Harvey Goldstein, Revised 19/12/2003
